12-та Европска женска математичка олимпијада (EGMO 2023)
Задача 4

 
Problem 4.
Turbo the snail sits on a point on a circle with circumference $1$. Given an infinite sequence of positive real numbers $c_1, c_2, c_3, \dots$, Turbo successively crawls distances $c_1, c_2, c_3, \dots$ around the circle, each time choosing to crawl either clockwise or counterclockwise.
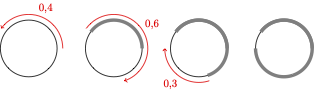
     For example, if the sequence c1, c2, c3, . . . is 0.4 , 0.6 , 0.3 , . . . , then Turbo may start crawling as follows:

     Determine the largest constant $C > 0$ with the following property: for every sequence of positive real numbers $c_1, c_2, c_3, \dots$ with $c_i < C$ for all $i$, Turbo can (after studying the sequence) ensure that there is some point on the circle that it will never visit or crawl across.